在外力作用下,物体的大小和形状都要发生变化,通常称之为形变。如果外力撤消后,物体能恢复原状,则这种性质称为物体的弹性;如果外力撤消后,物体不能恢复原状,则这种性质就称为物体的塑性。自然界既不存在完全弹性的物体,也不存在完全塑性的物体。对于任何物体,当外力小时,形变也小,外力撤消后,物体可完全复原;当外力大时,形变也大。若外力过大,形变超过一定限度,物体就不会复原了。这就说明,物体有一定的弹性限度,超过这个限度就变成塑性。与压电有关的问题,都属于弹性限度范围内的问题。因此,这里仅讨论物体的弹性性质。

一、应力

选两根长度相等,粗细不同的橡皮绳,当这两根橡皮绳受到相同的拉力作用时,显然,细橡皮绳比粗橡皮绳拉得长一些。为什么在相同的外力作用下,它们的伸长量不一样呢?这是因为两根橡皮绳的粗细不一样,也就是横截面的大小不样。由此可见,在拉力的作用下,物体的伸长量不仅与力的大小有关,而且还与物体的横截面的大小有关。为了计入横截面大小的影响,引入单位面积的作用力(即应力)这个概念,它的数学表达式为:

T=F/A

式中,T为应力,F为作用力,A为横截面(即力的作用面积)。通常规定作用力为拉力时,T>0,作用力为压力时,T<0。

二、应变

S= △1/1

式中,S为应变,l为原长,△l为伸长量,△l为单位长度的伸长量(或相对伸长量)。

三、正应力与正应变

如图2.2.1(a)所示的小方片,当它受到x方向的应力作用时,除在x方向产生伸长外,同时在y方向也产生收缩,如图2.2.1(b)所示。同样,当小方片受到y方向的应力作用时,除了在y方向产生伸长外,同时在x方向也产生收缩

如图2.2.1(c)所示。上述

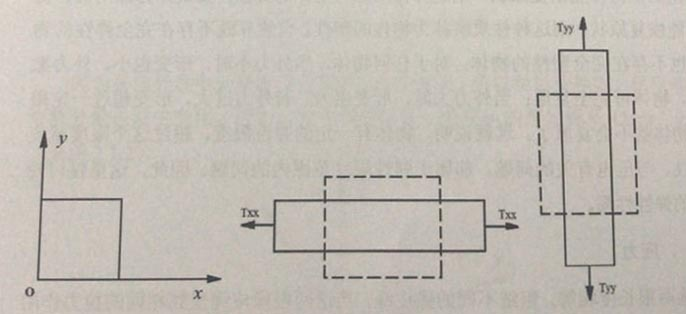
(a)未受力情况(b)沿x方向受力时的形变情况(c)沿y方向受力时的形变情况

图2.2.1小方片应力、应变示意图

沿x方向应力和y方向应力的特点是,力的方向与作用面垂直(或力的方向与作用面的法线方向平行)。为了反应这两个方向在应力符号上要附加两个足标,例如Tx和Ty。应力的第一个足标表示力的方向,第二个足标表示作用面的法线方向。同理,应变也有两个足标,例如Sx和Sy应变的第一个足标表示原长度的方向,第二个足标表示伸长量的方向,Tx、Ty又称正应力(或伸缩应力),Sx、Sy又称为正应变(或伸缩应变)为了简便,通常将足标中的(x,y,z)用(1,2,3)表示,而且将双足标简化为单足标,双足标与单足标的关系如表2.2.1所示。

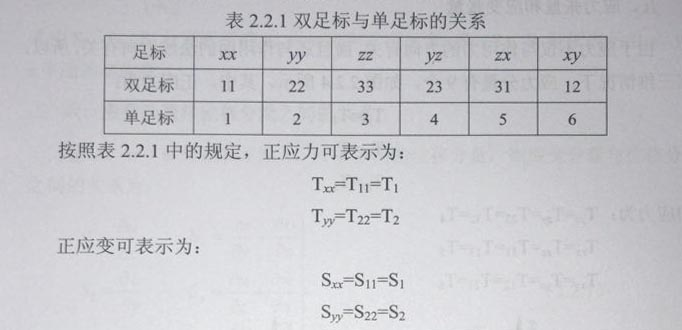
四、切应力与切应变

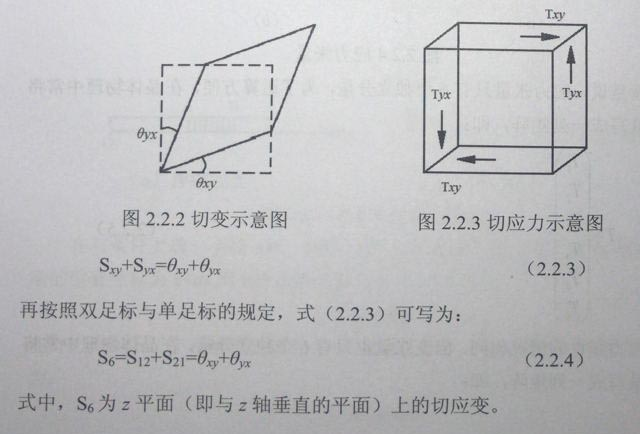
显然,S6这种切应变,在如图2.2.3所示的两对应力(Tyx,Tyx和Txy,Tyx)的作用下产生的,而这两对应力称为切应力。石英晶振,有源晶振,石英晶体谐振器等压电水晶元件切应力的特点是:力的方向与作用面平行,它可以使物体产生切变,而不能使物体产生转动,故有:

Tyx= Txy = T21 = T12 =T6

五、应力张量和应变张量

由于应力不仅与作用力的方向有关,而且还与作用面的法线方向有关,所以,在三维情况下,应力分量有9个,如图224所示。其中,正应力为:

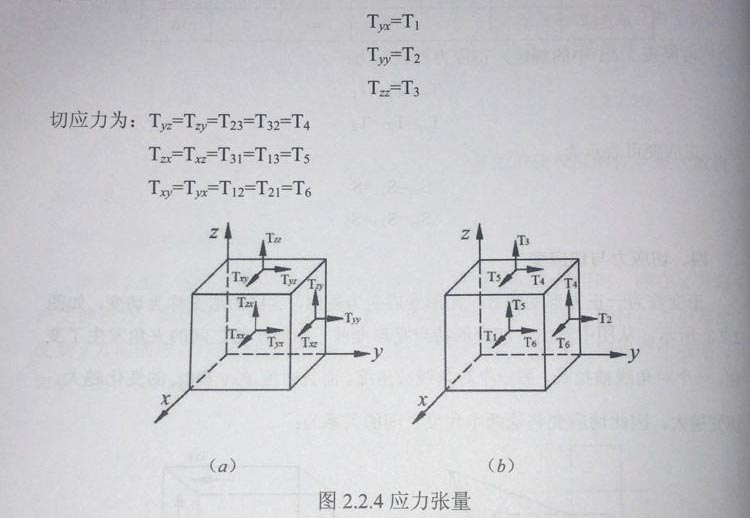
这就是说,应力张量只有6个独立分量,为了运算方便,在晶体物理中常将应力张量写成一列矩阵,即:

与应力张量的情况相同,应变张量也只有6个独立分量。在晶体物理中常将应变张量写成一列矩阵,即：

六、应变分量与位移分量之间的关系

设u、v、w分别表示沿x、y、z方向的位移分量,则应变分量与位移分量之间的关系为:

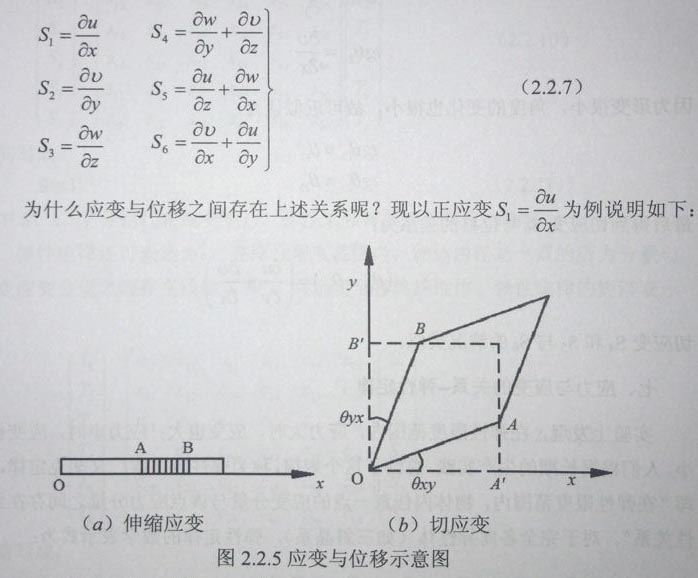
在石英杆上选一小段AB,如图22.5(a)所示,若A端的位置坐标为x,B端的位置坐标为x+dx,则AB小段的原长为:

x+dx-r=dx

在外力作用下,若A端的位移为u,B端的位移为u+dh,则AB两端的相对位移为

u+du-u=du

S₁=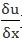正应变S2和S3与S1的情况类似。

再以切应变S6为例。根据切应变的定义:

切应变S4和S5与S6的情况类似。

七、应力与应变的关系一弹性定律

实验上发现,在弹性限度范围内,应力大时,应变也大;应力小时,应变也小。人们根据长期的生产实践,总结了这个规律,称为弹性定律或广义胡克定律,即“在弹性限度范围内,物体内任意一点的应变分量与该点应力分量之间存在线性关系”。对于完全各向异性体(如三斜晶系),弹性定律的数学表示式为:

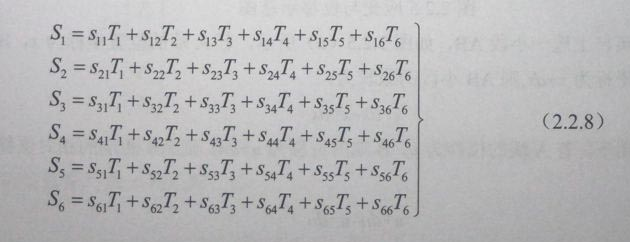
或简写成

式中系数S称为弹性柔顺常数,并有Sij=Sji(i≠j),由式(2.2.8)可以看出不仅正应力能产生正应变,而且切应力也能产生正应变;同样,不仅切应力能产生切应变,而且正应力也能产生切应变。这就是说,在一般情况下,应变与应力之间的关系是比较复杂的。

式(2.28)还可写成矩阵形式,即：

或简写成：

式中系数c称为弹性刚度常数;c代表弹性弹性刚度常数矩阵。